设计跳表, C语言实现

跳跃表简介

跳跃表是一种以O(log N)期望时间支持查找、插入、删除操作的、有序的数据结构。其性能和红黑树相当，且跳跃表实现更为简单。

如何理解”跳跃“二字

1. 首先，考察一个有序的单链表。如下图所示，该链表由8个元素组成，为了查找元素14，需要依次遍历 2 -> 4 -> 6 -> 8 -> 10 -> 12 -> 14, 共考察7个节点。考察的节点数正比于链表长度，查找的时间复杂度为O(n)，效率很低。

2. 为了加快查找速度，可以对单链表进行改造，每隔一个节点新增一个指针，指向它前面两个位置上的节点。所有新增的节点组成一条新的单链表(下图中的链表1)。同样查找元素14，现在只需考察4, 8, 12, 14，共4个节点。
   

3. 对链表1做类似的操作，又得到一条新的单链表(下图中的链表2)。此时查找元素14，只需考察8, 12, 14，共3个节点。

可以看出，跳跃表是由多条有序链表组成，支持折半查找的数据结构。

实现跳跃表

以下用C语言实现一个简单的跳表。跳表实现要求如下，详细参考：LeetCode 1206 设计跳表

• 需实现跳表创建、查找、插入、删除、释放等操作，不需实现区间查找。
• 跳表中的元素类型均为int。
• 跳表中可以存在多个相同的值。

0. 数据结构设计

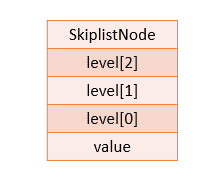
设计SkiplistNode结构表示跳跃表节点，如下：

typedef struct SkiplistNode {
	int value;							// 存储值
	struct SkiplistLevel {
		struct SkiplistNode *next;
	} level[];							// 层，这里设计成柔性数组，简化malloc和free操作
} SkiplistNode;

设计Skiplist结构持有这些跳跃表节点，如下：

typedef struct {
	struct SkiplistNode *head;			// 跳跃表表头节点
    int length;							// 跳跃表节点数，获取跳跃表长度的时间复杂度O(1)
    int level;							// 记录跳跃表内，层数最大的那个节点的层数。
} Skiplist;

• length表示跳跃表节点数，使得获取跳表长度的时间复杂度降为O(1)。
• level表示跳表层数，跳表的插入、删除操作需要读取和更新level的值。

下图表示一个层数为3的节点：

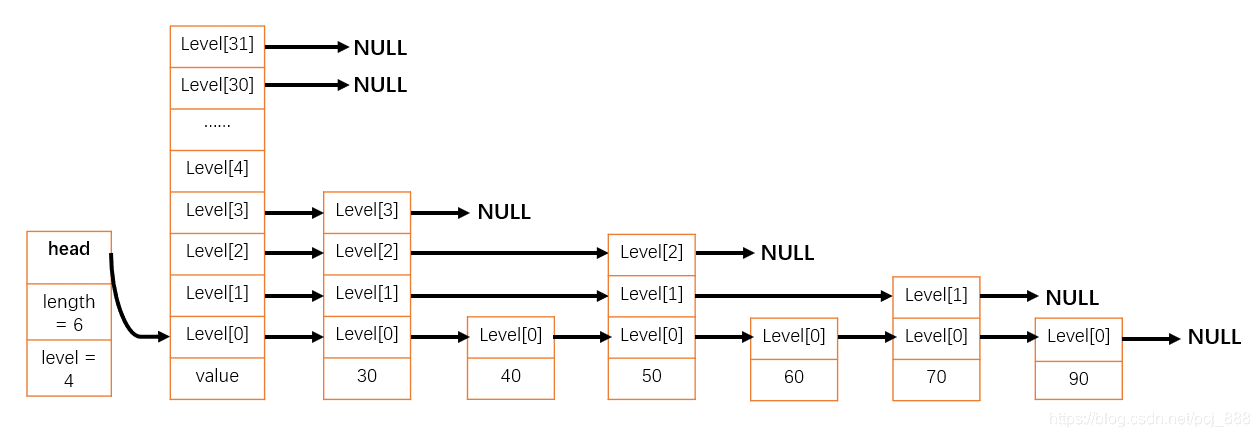
下图表示一个长度为6，层数为4的跳表：

1. 创建跳跃表

设计Skiplist* skiplistCreate()方法创建跳跃表，要点如下：

• 给Skiplist分配空间，长度初始为0，层高初始为1
• 创建并初始化跳表的附加头节点，并设置层高为SKIPLIST_MAXLEVEL(32)

#define SKIPLIST_MAXLEVEL 32
// 跳表的创建
Skiplist* skiplistCreate() {
    Skiplist *sl = (Skiplist *)malloc(sizeof(*sl));
    sl->length = 0;
    sl->level = 1;
    sl->head = skiplistNodeCreate(SKIPLIST_MAXLEVEL, INT_MIN); // 初始化表头节点的层高为32
    for (int i = 0; i < SKIPLIST_MAXLEVEL; ++i) {
        sl->head->level[i].next = NULL;		// 初始化表头节点
    }
    return sl;
}
// helper func
SkiplistNode* skiplistNodeCreate(int level, int value) {
    SkiplistNode *p = (SkiplistNode *)malloc(sizeof(*p) + sizeof(struct SkiplistLevel) * level);
    p->value = value;
    return p;
}

2. 查找

设计bool skiplistSearch(Skiplist* obj, int target)实现跳表的查找。

上面分析过，跳表就是由N条有序链表组成的，所以对跳表的查找相当于从高到低，依次在N条有序链表中查找。

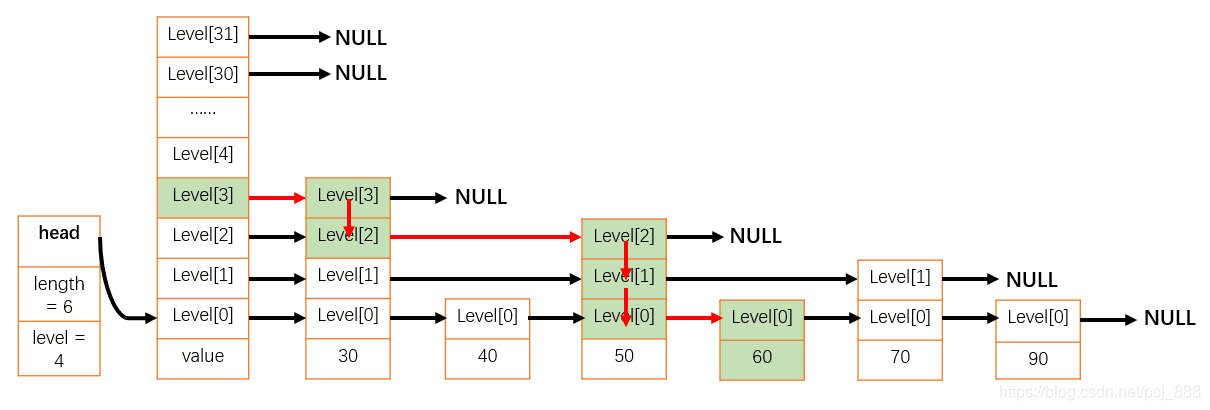
举例说明，在下图给出的跳表中，查找元素60，红色箭头表示遍历过程。

代码实现如下：

// 跳表的查找, 时间复杂度O(logN)
bool skiplistSearch(Skiplist* obj, int target) {
    SkiplistNode *p = obj->head;
    int levelIdx = obj->level - 1;
    for (int i = levelIdx; i >= 0; --i) {
        // 如果第i层节点值小于target, 就沿着当前层继续查找
        while (p->level[i].next && p->level[i].next->value < target) {
            p = p->level[i].next;
        }
        // 第i层未找到该节点, 或者节点值已大于target, 沿着下一层继续查找
        if (p->level[i].next == NULL || p->level[i].next->value > target) {
            continue;
        }
        return TRUE;
    }
    return FALSE;
}

3. 插入

设计void skiplistAdd(Skiplist* obj, int num)实现跳表的查找，要点如下：

• 新增节点时，确定这个新增节点的层高。
• 如果新增节点的层数为N，需对这N条单链表分别执行插入操作。
• 成功插入节点后，注意更新跳表的长度和层高。

3.1 如何确定新增节点的层高？

跳表使用抛硬币的思想决定一个新增节点的层高，即有1/2的概率层数为1，1/4的概率层数为2，1/8的概率层数为3，以此类推。 这里实现GetSkipNodeRandomLevel方法，确定新增节点层高，如下：

int GetSkipNodeRandomLevel() {
    int level = 1;
    while (rand() & 0x1) {					// 抛硬币思想，随机数为奇数的概率可认为是1/2
        ++level;
    }
    return min(level,SKIPLIST_MAXLEVEL); 	// 返回的最大层数不超过32
}

3.2 新增节点后，如何更新跳表中对应的N条单链表？

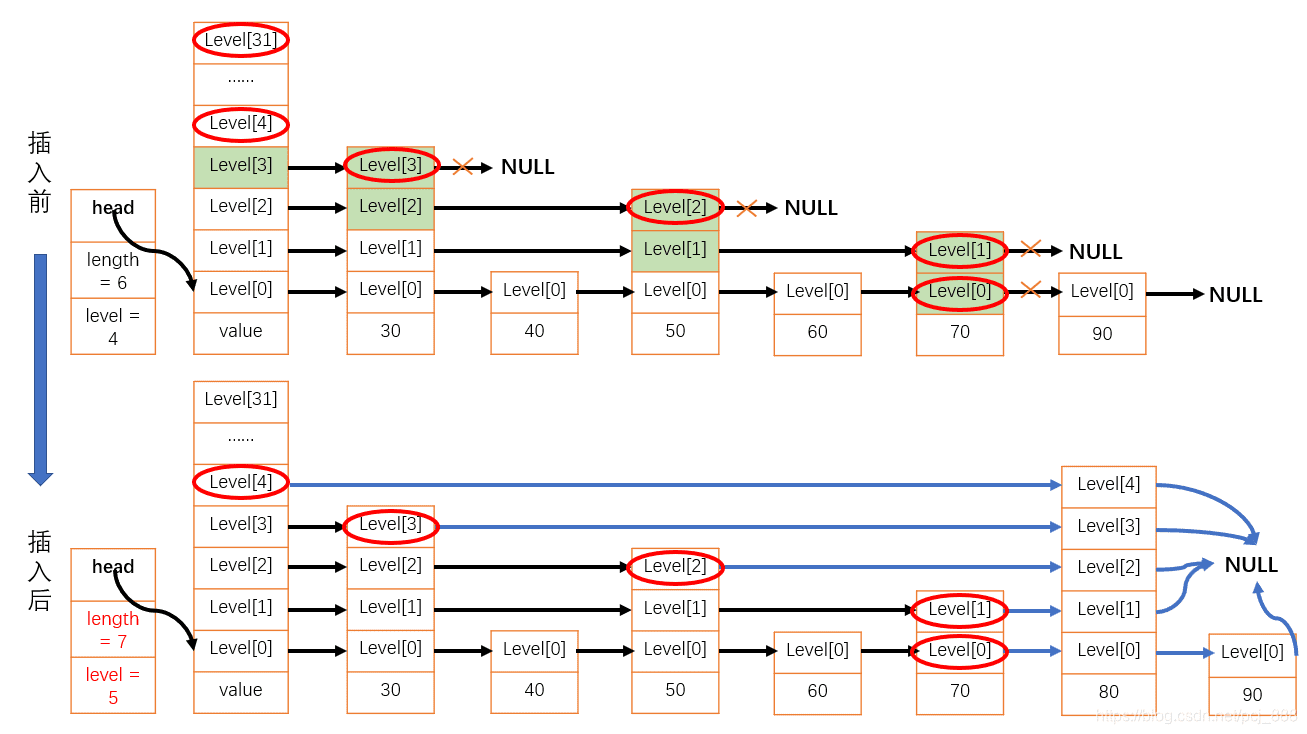
举例说明，给定一个包含6个元素，层数为4的跳表，现在新增一个节点值为80，层数为5，插入前后的变化如下：

可以看出，往跳表中插入元素，只需在遍历跳表的过程中，保存这5条链表待插入位置的前驱节点(红圈表示)，再分别对每条单链表执行插入操作即可，最后更新跳表的长度和层高。代码实现如下：

// 跳表的插入 O(logN)
void skiplistAdd(Skiplist* obj, int num) {
    SkiplistNode *p = obj->head;
    int levelIdx = obj->level - 1;
    struct SkiplistNode *preNodes[SKIPLIST_MAXLEVEL]; // 保存待插入节点的所有前驱节点的值
    for (int i = obj->level; i < SKIPLIST_MAXLEVEL; ++i) {
        preNodes[i] = obj->head;					  // 初始化值为附加头结点
    }

    for (int i = levelIdx; i >= 0; --i) {
        // 如果第i层节点值小于target, 沿当前层继续查找插入的位置
        while( p->level[i].next && p->level[i].next->value < num) {
            p = p->level[i].next;
        }
        preNodes[i] = p;
    }

    int newLevel = GetSkipNodeRandomLevel();		// 计算新插入节点的层数
    struct SkiplistNode *newNode = skiplistNodeCreate(newLevel, num);
    for (int i = 0; i < newLevel; ++i) {
        newNode->level[i].next = preNodes[i]->level[i].next;
        preNodes[i]->level[i].next = newNode;
    }
    obj->level = max(obj->level, newLevel);         // 完成插入动作后，更新跳跃表当前层数
    ++obj->length;									// 完成插入动作后，更新跳跃表长度
}

4. 删除

设计bool skiplistErase(Skiplist* obj, int num)方法实现跳表的删除，要点如下：

• 遍历跳表，确认待删除的值是否存在，这步和跳表的查找操作类似。
• 设待删除节点的层数为N，需对N条单链表分别执行删除操作。
• 成功删除节点后，注意更新跳表的长度和层高。

代码实现如下：

// 跳跃表删除操作 O(logN)
bool skiplistErase(Skiplist* obj, int num) {
    SkiplistNode *p = obj->head;
    int levelIdx = obj->level - 1;
    struct SkiplistNode *preNodes[SKIPLIST_MAXLEVEL]; // 存储所有待删除节点的前驱节点的值
    for (int i = levelIdx; i >= 0; --i) {
        // 如果第i层节点值小于num, 沿当前层继续查找
        while (p->level[i].next && p->level[i].next->value < num) {
            p = p->level[i].next;
        }
        preNodes[i] = p;
    }

    p = p->level[0].next;
    if (p && p->value == num) {	
        skiplistNodeDelete(obj, p, preNodes);
        return TRUE;
    }
    return FALSE;
}

void skiplistNodeDelete(Skiplist *obj, SkiplistNode *cur, SkiplistNode **preNodes)
{
    for (int i = 0; i < obj->level; ++i) {
        if (preNodes[i]->level[i].next == cur) { // 被删除的节点层数可能比跳表层数少，所以要加上这里的判断
            preNodes[i]->level[i].next = cur->level[i].next;
        }
    }
    // 如果删除的节点是层数最大的，那么可能需要更新跳表长度
    for (int i = obj->level - 1; i >= 1; --i) {
        if (obj->head->level[i].next != NULL) {
            break;
        }
        --obj->level;
    }
    --obj->length;
    // 释放被删除节点空间
    free(cur);
}

5. 跳表的释放

释放操作很简单。对于每个跳跃表节点，只需调1次free()即可。这也是SkiplistNode结构中level成员设计为柔性数组的好处。

void skiplistFree(Skiplist* obj) {
    SkiplistNode *cur = obj->head->level[0].next;
    SkiplistNode *d;
    while(cur) {
        d = cur;
        cur = cur->level[0].next;
        free(d);
    }
    free(obj->head);		   
    free(obj);
}

源码参考:https://leetcode-cn.com/problems/design-skiplist/solution/tiao-yue-biao-cyu-yan-shi-xian-by-pcj700

参考资料

【1】 Skip List–跳表

【2】《数据结构与算法分析 C语言描述》原书第2版 10.4.2 —— 跳跃表

【3】《Redis设计与实现》—— 第5章 跳跃表