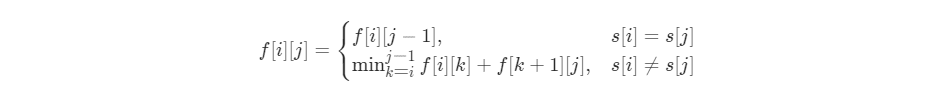题目描述
https://leetcode-cn.com/problems/strange-printer
解题思路
贪心法找不到明显思路,尝试动态规划求解。
1、 先明确动归问题的定义:
记f[i][j]为完成第i个字符到第j个字符的最少打印次数。记字符串s长度为n,则f[0][n-1]即为所求。
2、 将问题拆分成子问题,推导递推方程:
可以将区间[i, j]分解成[i, k],[k + 1, j] (其中i <= k < j),完成[i, j]打印问题转化为分别完成[i, k], [k + 1, j]两部分打印, k取值一共有j - i种可能,取最小的即可。递推方程:f[i][j] = min (k = i, k < j) f[i][k] + f[k+1][j]
3 、再考虑边界条件,缩小问题规模:
对于长度为1的区间,只需打印一次。对所有i都有,f[i][i] = 1
对于区间[i, j],如果第i个字符和第j个字符相等,可以在打印第i个字符时,顺便打印到右侧第j个字符,此时有f[i][j] = f[i][j - 1]
最终推导出状态转移方程:
![]()
代码实现
可以用记忆化搜索,或者自底向上法,代码如下:
记忆化搜索
套路就是用一个数组,在首次求解子问题时,保存(记忆)这个子问题的解,当再次求解相同子问题时,直接从数组里读取,避免重复递归。代码参考:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #define N_MAX 100
int g_strlen;
int dp[N_MAX][N_MAX];
int Dfs(char *s, int i, int j) {
if (i == j) {
return dp[i][i];
}
if (s[i] == s[j]) {
if (dp[i][j - 1] == 0) {
dp[i][j - 1] = Dfs(s, i, j - 1);
}
return dp[i][j - 1];
}
int minT = 0x3f3f3f3f;
int tmp;
for (int k = i; k < j; ++k) {
if (dp[i][k] == 0) {
dp[i][k] = Dfs(s, i, k);
}
if (dp[k + 1][j] == 0) {
dp[k + 1][j] = Dfs(s, k + 1, j);
}
tmp = dp[i][k] + dp[k + 1][j];
if (tmp < minT) {
minT = tmp;
}
}
return minT;
}
int strangePrinter(char * s){
g_strlen = strlen(s);
memset(dp, 0, sizeof(dp));
for (int i = 0; i < N_MAX; ++i) {
dp[i][i] = 1;
}
return Dfs(s, 0, g_strlen - 1);
}
|
自底向上法
相比记忆化搜索,自底向上法还需要考虑每个子问题的求解顺序。根据递推式,这里需从大到小去遍历i, 从小到大遍历j,就可以保证计算f[i][j]时,f[i][k] + f[k + 1][j]都被计算过。
优化点:s[i] != s[j]时剪枝,只有s[i]和s[k]相等时才计算,进一步压缩空间。代码参考:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| #define N_MAX 100
int dp[N_MAX][N_MAX];
int strangePrinter(char * s){
int str_len = strlen(s);
memset(dp, 0x3f, sizeof(dp));
int tmp;
for (int i = str_len - 1; i >= 0; --i) {
dp[i][i] = 1;
for (int j = i + 1; j < str_len; ++j) {
if (s[i] == s[j]) {
dp[i][j] = dp[i][j - 1];
continue;
}
for (int k = i; k < j; ++k) {
if (s[i] != s[k]) {
continue;
}
tmp = dp[i][k] + dp[k + 1][j];
if (tmp < dp[i][j]) {
dp[i][j] = tmp;
}
}
}
}
return dp[0][str_len - 1];
}
|
参考资料
LeetCode官方题解:https://leetcode-cn.com/problems/strange-printer/solution/qi-guai-de-da-yin-ji-by-leetcode-solutio-ogbu/